martes, 15 de agosto de 2017
lunes, 14 de agosto de 2017
sábado, 12 de agosto de 2017
viernes, 4 de agosto de 2017
PLANTILLA PARA CALCULO DEL ESALS - PAVIMENTOS
En esta oportunidad se compartirá una plantilla para el CALCULO DE ESALS - PAVIMENTOS, espero que sea de utilidad para ingenieros y estudiantes de la carrera de ingeniería civil.
Tu también puedes compartir material ingenieril con nosotros y en las publicaciones te daremos los créditos correspondientes.
Tu también puedes compartir material ingenieril con nosotros y en las publicaciones te daremos los créditos correspondientes.
DESCARGAR AQUÍ
PLANTILLA PARA EL DISEÑO Y ANÁLISIS DE VIGAS DE HORMIGÓN ARMADO
En esta oportunidad se compartirá una plantilla para el diseño y análisis de vigas de hormigón armado, espero que sea de utilidad para ingenieros y estudiantes de la carrera de ingeniería civil.
Tu también puedes compartir material ingenieril con nosotros y en las publicaciones te daremos los créditos correspondientes.
DESCARGAR AQUÍ
MS PROJECT: Microsoft Project 2013 - Curso Gratis
MS PROJECT: Microsoft Project 2013 - Curso Gratis: Compartimos 7 vídeos del Uso del software Ms Project 2013 Video 1: Configuracion y Primeros Pasos Video 2: Creación de Calendarios y...
PLANTILLA PARA ENCOFRADO DE COLUMNAS
Compartimos unas plantilla para el encofrado de columnas, las medidas están en (Pie2), esperamos que sea de utilidad para sus proyectos.
Un gran saludo al Autor por este gran aporte.
DESCARGA AQUÍ
MS PROJECT: Microsoft Project 2013 - Curso Gratis
MS PROJECT: Microsoft Project 2013 - Curso Gratis: Compartimos 7 vídeos del Uso del software Ms Project 2013 Video 1: Configuracion y Primeros Pasos Video 2: Creación de Calendarios y...
MS PROJECT: CURSO TALLER: Ms Project 2013 - MODULO II: Contro...
MS PROJECT: CURSO TALLER: Ms Project 2013 - MODULO II: Contro...: En Esta OPORTUNIDAD se Comparte Un Grupo de vídeos del software Microsoft Project 2013 dictado en el COLEGIO DE INGENIERO DEL PERÚ CD Junín ...
MODELADO DE RED DE AGUA - MÉTODO DE NEWTON-RAPHSON
MODELADO DE RED DE AGUA - MÉTODO DE NEWTON-RAPHSON
Este
documento explora el método de Newton-Raphson para resolver redes de agua
limpia. De hecho, este método numérico se utiliza en muchos programas de
ingeniería comercial actuales. Además, encontrará un ejemplo de un sistema
de red en bucle que resuelve completamente paso a paso.
Paso 1: Dibuje su red:
Paso 2:
Asumir
sus direcciones de flujo - en primer lugar, supongo:
Paso 3:
Defina
sus incógnitas de flujo:
- Q16 =
Q12 | 1 ST Desconocido
- Q25
| 2 nd Desconocido
- Q56
| 3 rd Desconocido
- Q34
| 4 º Desconocido
- Q45
| 5 º Desconocido
- Q23 | 6º Desconocido
Etapa 4:
Defina
sus ecuaciones:
2 bucles
= 2 ecuaciones:
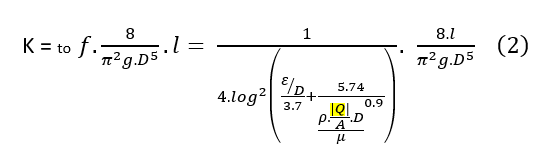
Las
pérdidas de la cabeza en una tubería se estiman como sigue usando la ecuación
de Darcy-Weisbach:
donde 'f' es el factor de fricción calculado usando la ecuación de Colebrook - white.
Así que
para el bucle 1, la ecuación es:
K16.Q16 2 +
K12.Q12 2 + K25.Q25 2 -K56.Q56 2 =
0, sustituir Q12 por Q16 porque Q12 = Q16
K16.Q16 2 + K12.Q16 2 + K25.Q25 2 -K56.Q56 2 = 0
La
ecuación para el bucle 2 es:
K23.Q23 2 +
K34.Q34 2 - K25.Q25 2 -K45.Q45 2 =
0
4 más
ecuaciones necesarias para resolver las 6 incógnitas, veamos algunos de
conservación de flujo:
Nodo
6> 25l / s - Q16 - Q56 = 0
Nodo
4> Q56 + Q25 - Q45 = 0
Nodo
2> Q12 - Q25 - Q23 = 0, Reemplace Q12 con Q16 porque Q12 = Q16
Q16 - Q25
- Q23 = 0
Nodo
3> Q23 - Q34 -10 = 0 Resumen de ecuaciones:
25l / s -
Q16 - Q56 = 0
Q56 + Q25 - Q45 = 0
Q16 - Q25 - Q23 = 0
Q23 - Q34 -10 = 0
K16.Q16 2 + K12.Q16 2 + K25.Q25 2 -K56.Q56 2 = 0
K23.Q23 2 + K34.Q34 2 - K25.Q25 2 -K45.Q45 2 = 0
Es muy
importante saber que las 6 ecuaciones anteriores requieren resolver usando el
método de Newton-Raphson a través de la matriz Jacobiana, pero debemos tener
cuidado al tratar con los valores de K en nuestra ecuación. Como se
mencionó anteriormente, cada valor de K depende del diámetro de la tubería y
del factor de fricción. El factor de fricción también
depende del caudal, por lo tanto, los valores de K deben ser reemplazados por
la ecuación explícita aproximada de Colebrook
- blanco. Si usted decide usar la forma implícita exacta de
la ecuación de Colebrook - white, entonces 7 ecuaciones implícitas adicionales de
Colebrook - white deberían agregarse a las 6 ecuaciones
anteriores. Afortunadamente tenemos las aproximaciones explícitas de
la ecuación de Colebrook - white y para el propósito de este
documento la usaremos. F: factor de fricción
L:
longitud, m
D:
diámetro, m
Q: caudal,
m $ ³ $
A: Área
de la sección transversal, m 2
ρ: Densidad, kg / m 3
G:
aceleración por gravedad, m / s 2
Etapa 5:
¿Cómo
resolver el sistema de ecuaciones usando el método de Netwon -Raphson?
Primero:
Es
necesario asumir los valores de la tasa de flujo desconocido; Esto se
llamará Trial 0.
Ensayo 0
suposición:
Segundo:
anote todos los parámetros de los enlaces, Diámetro y factores de rugosidad:
Enlace
1-2:
Diámetro = 0,6 m, Rugosidad = 0,000001
Enlace
2-3:
Diámetro
= 0,4 m, Rugosidad = 0,000001
Enlace
3-4:
Diámetro
= 0,2 m, Rugosidad = 0,000001
Enlace 4-5:
Diámetro = 0,3 m, Rugosidad = 0,000001
Enlace 6-5:
Diámetro
= 0,2 m, Rugosidad = 0,000001
Enlace
1-6:
Diámetro
= 0,6 m, Rugosidad = 0,000001
Enlace
2-5:
Diámetro
= 0,2 m, Rugosidad = 0,000001
Supongamos que todas las red en
este ejemplo tienen una longitud de 1m
Tercero:
Escriba la siguiente Matriz Jacobiana :
La matriz Jacobiana está hecha de la diferencial de las seis ecuaciones con respecto a los diferentes flujos desconocidos (Q)
Reemplace K por su equivalente según la ecuación (3), la función siguiente debe ser con respecto a Q.
La matriz
anterior será igual a:
El método
iterativo de Newton se define por:
Etapa 6:
La
inserción de los valores de los caudales del ensayo 1 en la matriz jacobiana
dará lo siguiente:
Vamos a
encontrar el inverso de la Matriz Jacobiana:
Un tercer ensayo se puede llevar
a cabo para reducir el% de error, pero la respuesta anterior es satisfactoria.